解谜计算机科学

要掌握一个学科的精髓，不能从细枝末节开始。人脑的能力很大程度上受限于信念。一个人不相信自己的时候，他就做不到本来可能的事。信心是很重要的，信心却容易被挫败。如果只见树木不见森林，人会失去信心，以为要到猴年马月才能掌握一个学科。

精辟, 信心是万物之始.
将表达式纳入到考虑的范围. 计算图, 模型, 符号

所以我们不从“树木”开始，而是引导读者一起来探索这背后的“森林”，把计算机科学最根本的概念用浅显的例子解释，让读者领会到它们的本质。把这些概念稍作发展，你就得到逐渐完整的把握。你一开头就掌握着整个学科，而且一直掌握着它，只不过增添更多细节而已。这就像画画，先勾勒出轮廓，一遍遍的增加细节，日臻完善，却不失去对大局的把握。

一般计算机专业的学生学了很多课程，可是直到毕业都没能回答一个基础问题：什么是计算？这一章会引导你去发现这个问题的答案。不要小看这基础的问题，它经常是解决现实问题的重要线索。世界上有太多不理解它的人，他们走了很多的弯路，掉进很多的坑，制造出过度复杂或者有漏洞的理论和技术。

接下来，我们就来理解几个关键的概念，由此接触到计算的本质。

手指算术

每个人都做过计算，只是大部分人都没有理解自己在做什么。回想一下幼儿园（大概四岁）的时候，妈妈问你：“帮我算一下，4+3 等于几？” 你掰了一会手指，回答：7。当你掰手指的时候，你自己就是一台简单的计算机。

不要小看了这手指算术，它蕴含着深刻的原理。计算机科学植根于这类非常简单的过程，而不是复杂的高等数学。

现在我们来回忆一下这个过程。这里应该有一段动画，但现阶段还没有。请你对每一步发挥一下想象力，增加点“画面感”。

当妈妈问你“4+3 等于几”的时候，她是一个程序员，你是一台计算机。计算机得到程序员的输入：4，+，3。
听到妈妈的问题之后，你拿出两只手，左手伸出四个指头，右手伸l出三个指头。
接着你开始自己的计算过程。一根根地数那些竖起来的手指，每数一根你就把它弯下去，表示它已经被数过了。你念道：“1，2，3，4，5，6，7。”
现在已经没有手指伸着，所以你把最后数到的那个数作为答案：7！整个计算过程就结束了。

符号和模型

这里的幼儿园手指算术包含着深刻的哲学问题，现在我们来初步体会一下这个问题。

当妈妈说“帮我算 4+3”的时候，4，+，3，三个字符传到你耳朵里，它们都是符号（symbol）。符号是“表面”的东西：光是盯着“4”和“3”这两个阿拉伯数字的曲线，一个像旗子，一个像耳朵，你是不能做什么的。你需要先用脑子把它们转换成对应的“模型”（model）。这就是为什么你伸出两只手，一只手表示 4，另一只表示 3。

这两只手的手势是“可操作”的。比如，你把左手再多弯曲一个手指，它就变成“3”。你再伸开一根手指，它就变成“5”。所以手指是一个相当好的机械模型，它是可以动，可操作的。把符号“4”和“3”转换成手指模型之后，你就可以开始计算了。

你怎么知道“4”和“3”对应什么样的手指模型呢？因为妈妈以前教过你。十根手指，对应着 1 到 10 十个数。这就是为什么人都用十进制数做算术。

我们现在没必要深究这个问题。我只是提示你，分清“符号”和“模型”是重要的。

计算图

在计算机领域，我们经常用一些抽象的图示来表达计算的过程，这样就能直观地看到信息的流动和转换。这种图示看起来是一些形状用箭头连接起来。我在这里把它叫做“计算图”。

对于以上的手指算术 4 + 3，我们可以用下图来表示它：

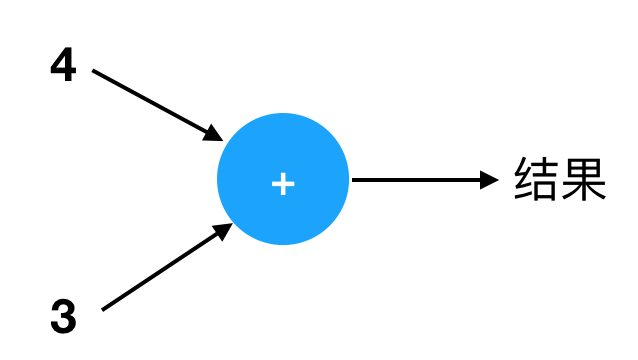
图中的箭头表示信息的流动方向。说到“流动”，你可以想象一下水的流动。首先我们看到数字 4 和 3 流进了一个圆圈，圆圈里有一个“+”号。这个圆圈就是你，一个会做手指加法的小孩。妈妈给你两个数 4 和 3，你现在把它们加起来，得到 7 作为结果。

注意圆圈的输入和输出方向是由箭头决定的，我们可以根据需要调整那些箭头的位置，只要箭头的连接关系和方向不变就行。它们不一定都是从左到右，也可能从右到左或者从上到下，但“出入关系”都一样：4 和 3 进去，结果 7 出来。比如它还可以是这样：

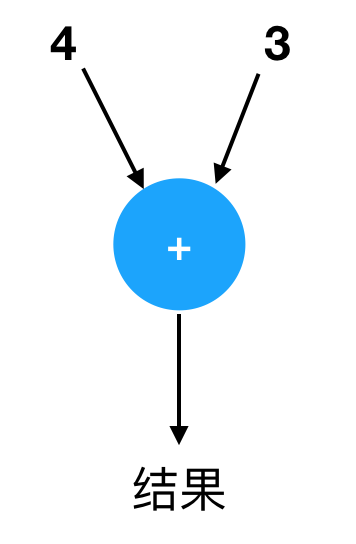
我们用带加号的圆圈表示一个“加法器”。顾名思义，加法器可以帮我们完成加法。在上个例子里，你就是一个加法器。我们也可以用其他装置作为加法器，比如一堆石头，一个算盘，某种电子线路…… 只要它能做加法就行。

具体要怎么做加法，就像你具体如何掰手指，很多时候我们是不关心的，我们只需要知道这个东西能做加法就行。圆圈把具体的加法操作给“抽象化”了，这个蓝色的圆圈可以代表很多种东西。抽象（abstraction）是计算机科学至关重要的思维方法，它帮助我们进行高层面的思考，而不为细节所累。

表达式

计算机科学当然不止 4 + 3 这么简单，但它的基本元素确实是如此简单。我们可以创造出很复杂的系统，然而归根结底，它们只是在按某种顺序计算像 4 + 3 这样的东西。

4 + 3 是一个很简单的表达式（expression）。你也许没听说过“表达式”这个词，但我们先不去定义它。我们先来看一个稍微复杂一些的表达式：

1	2 * (4 + 3)

这个表达式比 4 + 3 多了一个运算，我们把它叫做“复合表达式”。这个表达式也可以用计算图来表示：

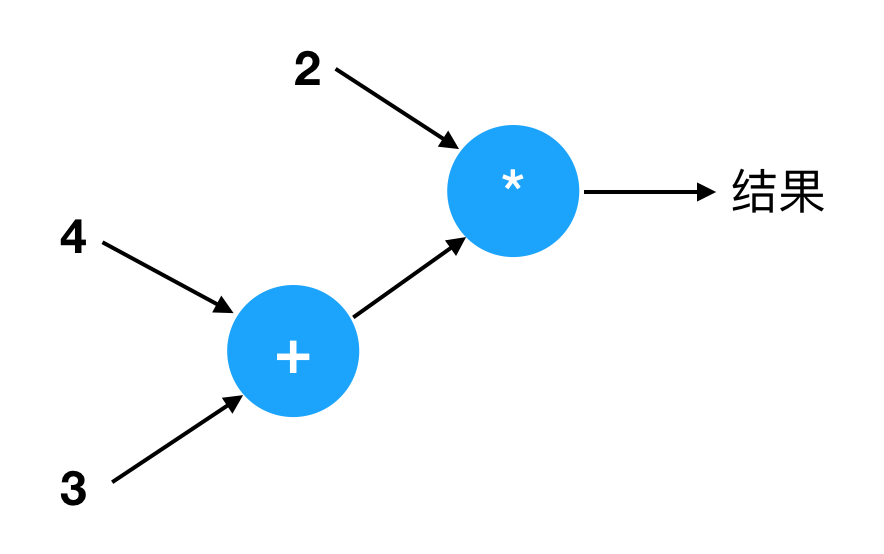
你知道它为什么是这个样子吗？它表示的意思是，先计算 4 + 3，然后把结果（7）传送到一个“乘法器”，跟 2 相乘，得到最后的结果。那正好就是 2 * (4 + 3) 这个表达式的含义，它的结果应该是 14。

为什么要先计算 4 + 3 呢？因为当我们看到乘法器 2 * ... 的时候，其中一个输入（2）是已知的，而另外一个输入必须通过加法器的输出得到。加法器的结果是由 4 和 3 相加得到的，所以我们必须先计算 4 + 3，然后才能与 2 相乘。

小学的时候，你也许学过：“括号内的内容要先计算”。其实括号只是“符号层”的东西，它并不存在于计算图里面。我这里讲的“计算图”，其实才是本质的东西。数学的括号一类的东西，都只是表象，它们是符号或者叫“语法”。从某种意义上讲，计算图才是表达式的本质或者“模型”，而“2 * (4 + 3)”这串符号，只是对计算图的一种表示或者“编码”（coding）。

这里我们再次体会到了“符号”和“模型”的差别。符号是对模型的“表示”或者“编码”。我们必须从符号得到模型，才能进行操作。这种从符号到模型的转换过程，在计算机科学里叫做“语法分析”（parsing）。我们会在后面的章节理解这个过程。

我们现在来给表达式做一个初步的定义。这并不是完整的定义，但你应该试着理解这种定义的方式。稍后我们会逐渐补充这个定义，逐渐完善。

定义（表达式）：表达式可以是如下几种东西。

数字是一个表达式。比如 1，2，4，15，……
表达式 + 表达式。两个表达式相加，也是表达式。
表达式 - 表达式。两个表达式相减，也是表达式。
表达式 * 表达式。两个表达式相乘，也是表达式。
表达式 / 表达式。两个表达式相除，也是表达式。

注意，由于我们之前讲过的符号和模型的差别，为了完全忠于我们的本质认识，这里的“表达式 + 表达式”虽然看起来是一串符号，它必须被想象成它所对应的模型。当你看到“表达式”的时候，你的脑子里应该浮现出它对应的计算图，而不是一串符号。这个计算图的画面大概是这个样子，其中左边的大方框里可以是任意两个表达式。

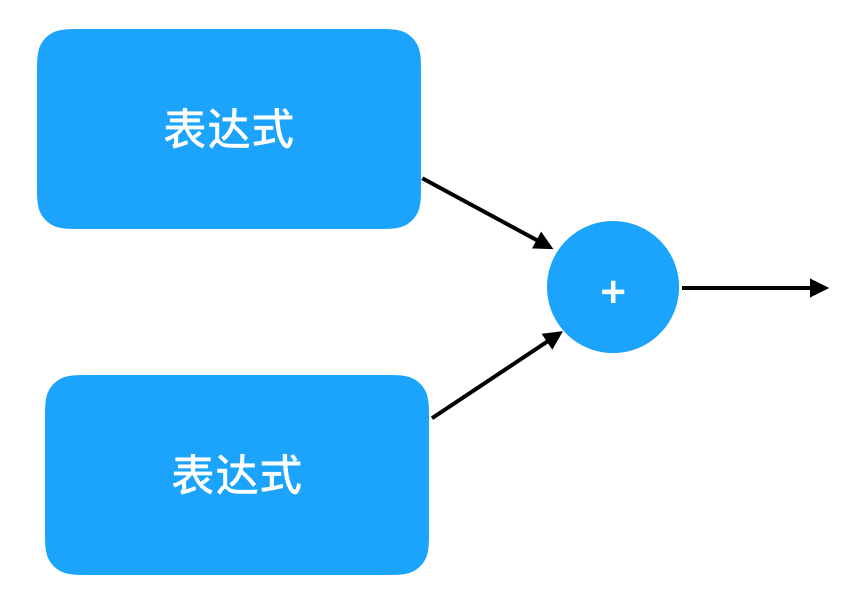
是不是感觉这个定义有点奇怪？因为在“表达式”的定义里，我们用到了“表达式”自己。这种定义叫做“递归定义”。所谓递归（recursion），就是在一个东西的定义里引用这个东西自己。看上去很奇怪，好像绕回去了一样。递归是一个重要的概念，我们会在将来深入理解它。

现在我们可以来验证一下，根据我们的定义，2 * (4 + 3) 确实是一个表达式：

首先根据第一种形式，我们知道 4 是表达式，因为它是一个数字。3 也是表达式，因为它是一个数字。
所以 4 + 3 是表达式，因为 + 的左右都是表达式，它满足表达式定义的第二种形式。
所以 2 * (4 + 3) 是表达式，因为 * 的左右都是表达式，它满足表达式定义的第四种形式。

并行计算

考虑这样一个表达式：

1	(4 + 3) * (1 + 2)

它对应一个什么样的计算图呢？大概是这样：

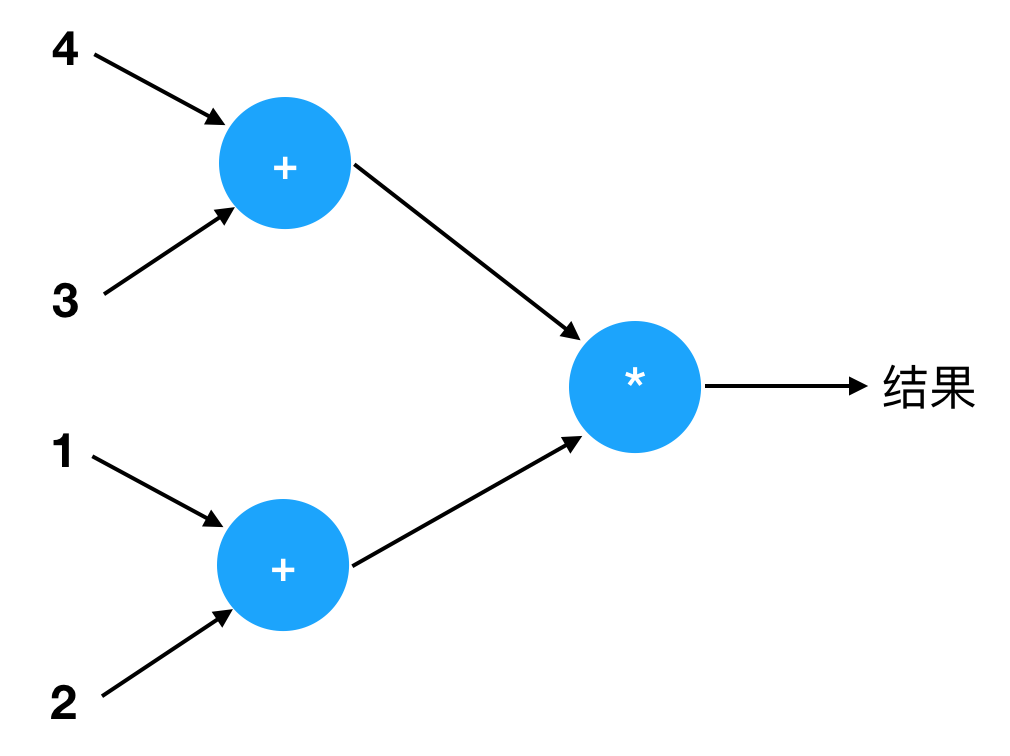
如果妈妈只有你一个小孩，你应该如何用手指算出它的结果呢？你大概有两种办法。

第一种办法：先算出 4+3，结果是 7。然后算出 1+2，结果是 3。然后算 7*3，结果是 21。

第二种办法：先算出 1+2，结果是 3。然后算出 4+3，结果是 7。然后算 7*3，结果是 21。

注意到没有，你要么先算 4+3，要么先算 1+2，你不能同时算 4+3 和 1+2。为什么呢？因为你只有两只手，所以算 4+3 的时候你就没法算 1+2，反之也是这样。总之，你妈妈只有你一个加法器，所以一次只能做一个加法。

现在假设你还有一个妹妹，她跟你差不多年纪，她也会手指算术。妈妈现在就多了一些办法来计算这个表达式。她可以这样做：让你算 4+3，不等你算完，马上让妹妹算 1+2。等到你们的结果（7 和 3）都出来之后，让你或者妹妹算 7*3。

发现没有，在某一段时间之内，你和妹妹同时在做加法计算。这种时间上重叠的计算，叫做并行计算（parallel computing）。

你和妹妹同时计算，得到结果的速度可能会比你一个人算更快。如果你妈妈还有其它几个孩子，计算复杂的式子就可能快很多，这就是并行计算潜在的好处。所谓“潜在”的意思是，这种好处不一定会实现。比如，如果你的妹妹做手指算数的速度比你慢很多，你做完了 4+3，只好等着她慢慢的算 1+2。这也许比你自己依次算 4+3 和 1+2 还要慢。

即使妹妹做算术跟你一样快，这里还有个问题。你和妹妹算出结果 7 和 3 之后，得把结果传递给下一个计算 7*3 的那个人（也许是你，也许是你妹妹）。这种“通信”会带来时间的延迟，叫做“通信开销”。如果你们其中一个说话慢，这比起一个人来做计算可能还要慢。

如何根据计算单元能力的不同和通信开销的差异，来最大化计算的效率，降低需要的时间，就成为了并行计算领域研究的内容。并行计算虽然看起来是一个“博大精深”的领域，可是你如果理解了我这里说的那点东西，就很容易理解其余的内容。

变量和赋值

如果你有一个复杂的表达式，比如

1	(5 - 3) * (4 + (2 * 3 - 5) * 6)

由于它有比较多的嵌套，人的眼睛是难以看清楚的，它要表达的意义也会难懂。这时候，你希望可以用一些“名字”来代表中间结果，这样表达式就更容易理解。

打个比方，这就像你有一个亲戚，他是你妈妈的表姐的女儿的丈夫。你不想每次都称他“我妈妈的表姐的女儿的丈夫”，所以你就用他的名字“叮当”来指代他，一下子就简单了。

我们来看一个例子。之前的复合表达式

1	2 * (4 + 3)

其实可以被转换为等价的，含有变量的代码：

{
    a = 4 + 3       // 变量 a 得到 4+3 的值
    2 * a           // 代码块的值
}

其中 a 是一个名字。a = 4 + 3 是一个“赋值语句”，它的意思是：用 a 来代表 4 + 3 的值。这种名字，计算机术语叫做变量（variable）。

这段代码的意思可以简单地描述为：计算 4 + 3，把它的结果表示为 a，然后计算 2 * a作为最后的结果。

有些东西可能扰乱了你的视线。两根斜杠 // 后面一直到行末的文字叫做“注释”，是给人看的说明文字。它们对代码的逻辑不产生作用，执行的时候可以忽略。许多语言都有类似这种注释，它们可以帮助阅读的人，但是会被机器忽略。

这段代码执行过程会是这样：先计算 4 + 3 得到 7，用 a 记住这个中间结果 7。接着计算 2 * a ，也就是计算 2 * 7，所以最后结果是 14。很显然，这跟 2 * (4 + 3) 的结果是一样的。

a 叫做一个变量，它是一个符号，可以用来代表任意的值。除了 a，你还有许多的选择，比如 b, c, d, x, y, foo, bar, u21… 只要它不会被误解成其它东西就行。

如果你觉得这里面的“神奇”成分太多，那我们现在来做更深一层的理解……

再看一遍上面的代码。这整片代码叫做一个“代码块”（block），或者叫一个“序列”（sequence）。这个代码块包括两条语句，分别是 a = 4 + 3 和 2 * a。代码块里的语句会从上到下依次执行。所以我们先执行 a = 4 + 3，然后执行 2 * a。

最后一条语句 2 * a 比较特别，它是这个代码块的“值”，也就是最后结果。之前的语句都是在为生成这个最后的值做准备。换句话说，这整个代码块的值就是 2 * a 的值。不光这个例子是这样，这是一个通用的原理：代码块的最后一条语句，总是这个代码块的值。

我们在代码块的前后加上花括号 {...} 进行标注，这样里面的语句就不会跟外面的代码混在一起。这两个花括号叫做“边界符”。我们今后会经常遇到代码块，它存在于几乎所有的程序语言里，只是语法稍有不同。比如有些语言可能用括号 (...) 或者 BEGIN...END来表示边界，而不是用花括号。

这片代码已经有点像常用的编程语言了，但我们暂时不把它具体化到某一种语言。我不想固化你的思维方式。在稍后的章节，我们会把这种抽象的表达法对应到几种常见的语言，这样一来你就能理解几乎所有的程序语言。

另外还有一点需要注意，同一个变量可以被多次赋值。它的值会随着赋值语句而改变。举个例子：

{
    a = 4 + 3
    b = a
    a = 2 * 5
    c = a
}

这段代码执行之后，b 的值是 7，而 c 的值是 10。你知道为什么吗？因为 a = 4 + 3 之后，a 的值是 7。b = a 使得 b 得到值 7。然后 a = 2 * 5 把 a 的值改变了，它现在是 10。所以 c = a 使得 c 得到 10。

对同一个变量多次赋值虽然是可以的，但通常来说这不是一种好的写法，它可能引起程序的混淆，应该尽量避免。只有当变量表示的“意义”相同的时候，你才应该对它重复赋值。

编译

一旦引入了变量，我们就可以不用复合表达式。因为你可以把任意复杂的复合表达式拆开成“单操作算术表达式”（像 4 + 3 这样的），使用一些变量记住中间结果，一步一步算下去，得到最后的结果。

举一个复杂点的例子，也就是这一节最开头的那个表达式：

1	(5 - 3) * (4 + (2 * 3 - 5) * 6)

它可以被转化为一串语句：

{
    a = 2 * 3
    b = a - 5
    c = b * 6
    d = 4 + c
    e = 5 - 3
    e * d
}

最后的表达式 e * d，算出来就是原来的表达式的值。你观察一下，是不是每个操作都非常简单，不包含嵌套的复合表达式？你可以自己验算一下，它确实算出跟原表达式一样的结果。

在这里，我们自己动手做了“编译器”（compiler）的工作。通常来说，编译器是一种程序，它的任务是把一片代码“翻译”成另外一种等价形式。这里我们没有写编译器，可是我们自己做了编译器的工作。我们手动地把一个嵌套的复合表达式，编译成了一系列的简单算术语句。

这些语句的结果与原来的表达式完全一致。这种保留原来语义的翻译过程，叫做编译（compile）。

我们为什么需要编译呢？原因有好几种。我不想在这里做完整的解释，但从这个例子我们可以看到，编译之后我们就不再需要复杂的嵌套表达式了。我们只需要设计很简单的，只会做单操作算术的机器，就可以算出复杂的嵌套的表达式。实际上最后这段代码已经非常接近现代处理器（CPU）的汇编代码（assembly）。我们只需要多加一些转换，它就可以变成机器指令。

我们暂时不写编译器，因为你还缺少一些必要的知识。这当然也不是编译技术的所有内容，它还包含另外一些东西。但从这一开头，你就已经初步理解了编译器是什么，你只需要在将来加深这种理解。

函数

到目前为止，我们做的计算都是在已知的数字之上，而在现实的计算中我们往往有一些未知数。比如我们想要表达一个“风扇控制器”，有了它之后，风扇的转速总是当前气温的两倍。这个“当前气温”就是一个未知数。

我们的“风扇控制器”必须要有一个“输入”（input），用于得到当前的温度 t，它是一个温度传感器的读数。它还要有一个输出，就是温度的两倍。

那么我们可以用这样的方式来表达我们的风扇控制器：

t -> t*2

不要把这想成任何一种程序语言，这只是我们自己的表达法。箭头 -> 的左边表示输入，右边表示输出，够简单吧。

你可以把 t 想象成从温度传感器出来的一根电线，它连接到风扇控制器上，风扇控制器会把它的输入（t）乘以 2。这个画面像这个样子：

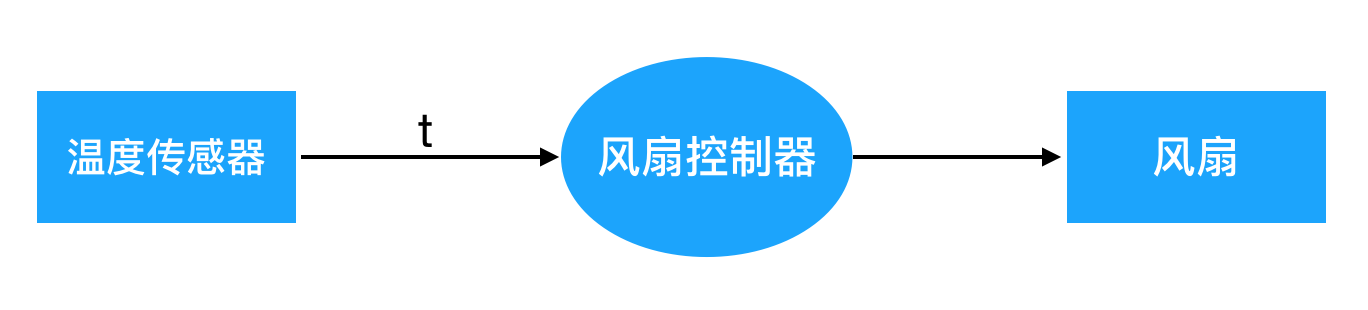
我们谈论风扇控制器的时候，其实不关心它的输入是哪里来的，输出到哪里去。如果我们把温度传感器和风扇从画面里拿掉，就变成这个样子：

这幅图才是你需要认真理解的函数的计算图。你发现了吗，这幅图画正好对应了之前的风扇控制器的符号表示：t -> t*2。看到符号就想象出画面，你就得到了符号背后的模型。

像 t -> t*2 这样具有未知数作为输入的构造，我们把它叫做函数（function）。其中 t 这个符号，叫做这个函数的参数。

参数，变量和电线

你可能发现了，函数的参数和我们之前了解的“变量”是很类似的，它们都是一个符号。之前我们用了 a, b, c, d, e 现在我们有一个 t，这些名字我们都是随便起的，只要它们不要重复就好。如果名字重复的话，可能会带来混淆和干扰。

其实参数和变量这两种概念不只是相似，它们的本质就是一样的。如果你深刻理解它们的相同本质，你的脑子就可以少记忆很多东西，而且它可能帮助你对代码做出一些有趣而有益的转化。在上一节你已经看到，我用“电线”作为比方来帮助你理解参数。你也可以用同样的方法来理解变量。

比如我们之前的变量 a：

{
    a = 4 + 3
    2 * a
}

它可以被想象成什么样的画面呢？

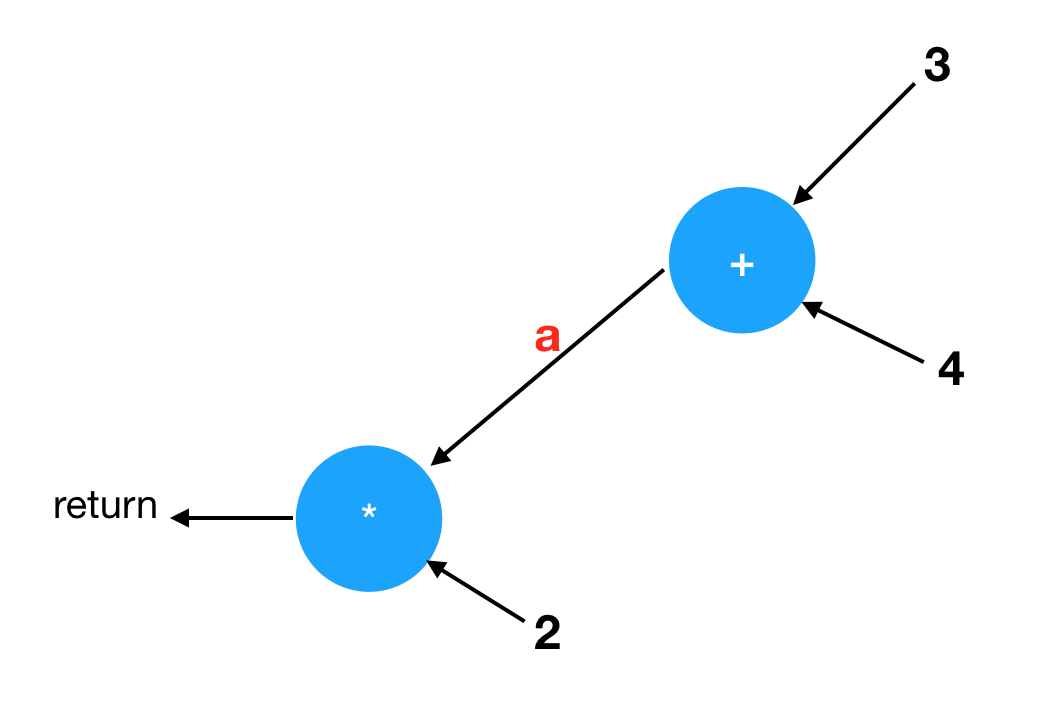
我故意把箭头方向画成从右往左，这样它就更像上面的代码。从这个图画里，你也许可以看到变量 a 和风扇控制器图里的参数 t，其实没有任何本质差别。它们都表示一根电线，那根电线进入乘法器，将会被乘以 2，然后输出。如果你把这些都看成是电路，那么变量 a 和参数 t 都代表一根电线而已。

然后你还发现一个现象，那就是你可以把 a 这个名字换成任何其它名字（比如 b），而这幅图不会产生实质的改变。

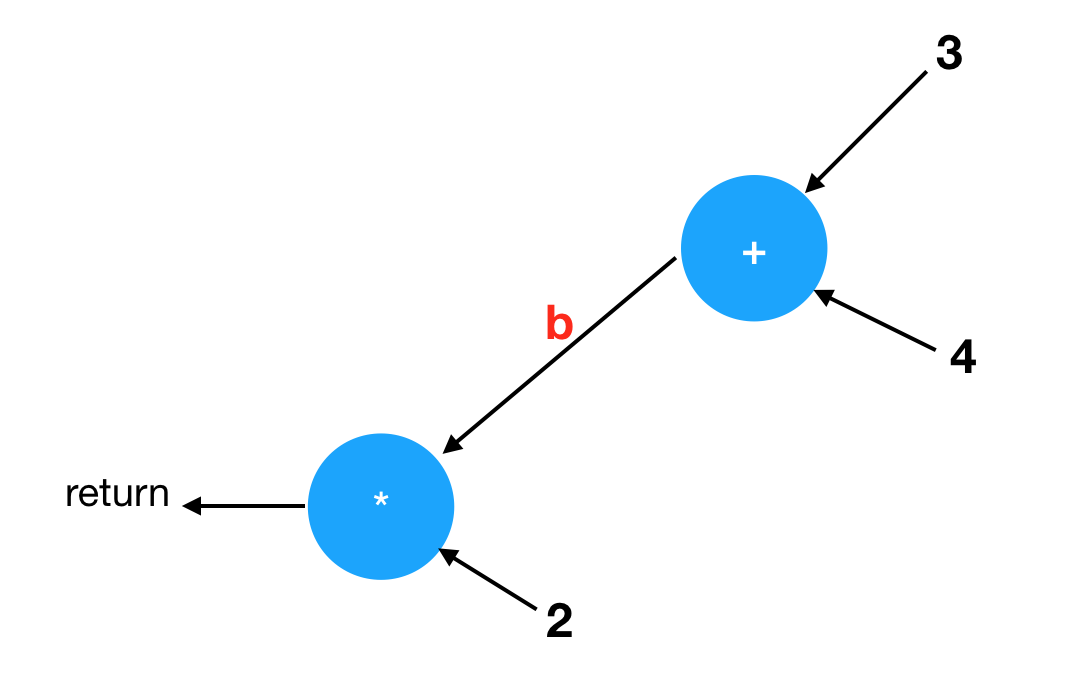
这说明什么问题呢？这说明以下的代码（把 a 换成了 b）跟之前的是等价的：

{
    b = 4 + 3
    2 * b
}

根据几乎一样的电线命名变化，你也可以对之前的函数得到一样的结论：t -> t*2 和 u -> u*2，和 x -> x*2 都是一回事。

名字是很重要的东西，但它们具体叫什么，对于机器并没有实质的意义，只要它们不要相互混淆就可以。但名字对于人是很重要的，因为人脑没有机器那么精确。不好的变量和参数名会导致代码难以理解，引起程序员的混乱和错误。所以通常说来，你需要给变量和参数起好的名字。

什么样的名字好呢？我会在后面集中讲解。

有名字的函数

既然变量可以代表“值”，那么一个自然的想法，就是让变量代表函数。所以就像我们可以写

a = 4 + 3

我们似乎也应该可以写

1	f = t -> t*2

对的，你可以这么做。f = t->t*2 还有一个更加传统的写法，就像数学里的函数写法：

1	f(t) = t*2

请仔细观察 t 的位置变化。我们在函数名字的右边写一对括号，在里面放上参数的名字。

注意，你不可以只写

f = t*2

你必须明确的指出函数的参数是什么，否则你就不会明白函数定义里的 t 是什么东西。明确指出 t 是一个“输入”，你才会知道它是函数的输入，是一个未知数，而不是在函数外面定义的其它变量。

这个看似简单的道理，很多数学家都不明白，所以他们经常这样写书：

有一个函数 y = x*2

这是错误的，因为他没有明确指出“x 是函数 y 的参数”。如果这句话之前他们又定义过 x，你就会疑惑这是不是之前那个 x。很多人就是因为这些糊里糊涂的写法而看不懂数学书。这不怪他们，只怪数学家自己对于语言不严谨。

函数调用

有了函数，我们可以给它起名字，可是我们怎么使用它的值呢？

由于函数里面有未知数（参数），所以你必须告诉它这些未知数，它里面的代码才会执行，给你结果。比如之前的风扇控制器函数

1	f(t) = t*2

它需要一个温度作为输入，才会给你一个输出。于是你就这样给它一个输入：

f(2)

你把输入写在函数名字后面的括号里。那么你就会得到输出：4。也就是说 f(2) 的值是 4。

如果你没有调用一个函数，函数体是不会被执行的。因为它不知道未知数是什么，所以什么事也做不了。那么我们定义函数的时候，比如

1	f(t) = t*2

当看到这个定义的时候，机器应该做什么呢？它只是记录下：有这么一个函数，它的参数是 t，它需要计算 t*2，它的名字叫 f。但是机器不会立即计算 t*2，因为它不知道 t 是多少。

分支

直到现在，我们的代码都是从头到尾，闷头闷脑地执行，不问任何问题。我们缺少一种“问问题”的方法。比如，如果我想表达这样一个“食物选择器”：如果气温低于 22 度，就返回 “hotpot” 表示今天吃火锅，否则返回 “ice cream” 表示今天吃冰激凌。

我们可以把它图示如下：

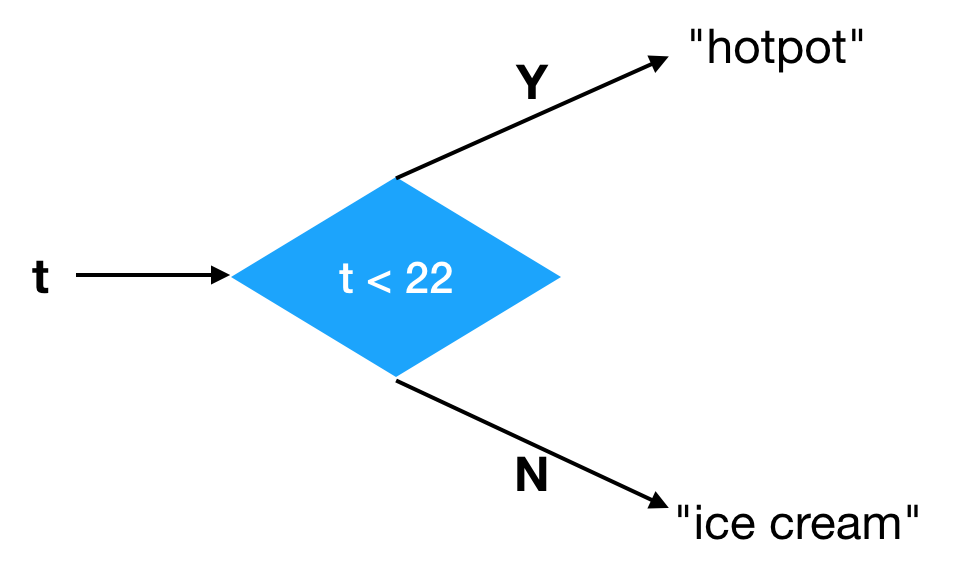
中间这种判断结构叫做“分支”（branching），它一般用菱形表示。为什么叫分支呢？你想象一下，代码就像一条小溪，平时它沿着一条路线流淌。当它遇到一个棱角分明的大石头，就分成两个支流，分开流淌。

我们的判断条件 t < 22 就像一块大石头，我们的“代码流”碰到它就会分开成两支，分别做不同的事情。跟溪流不同的是，这种分支不是随机的，而是根据条件来决定，而且分支之后只有一支继续执行，而另外一边不会被执行。

我们现在看到的都是图形化表示的模型，为了书写方便，现在我们要从符号的层面来表示这个模型。我们需要一种符号表示法来表达分支，我们把它叫做 if（如果）。我们的饮料选择器代码可以这样写：

t -> if (t < 22) 
     {
       "hotpot"
     }
     else 
     {
       "ice cream"
     }

它是一个函数，输入是一个温度。if 后面的括号里放我们的判断条件。后面接着条件成立时执行的代码块，然后是一个 else，然后是条件不成立时执行的代码。它说：如果温度低于 22 度，我们就吃火锅，否则就吃冰激凌。

其中的 else 是一个特殊的符号，它表示“否则”。看起来不知道为什么 else 要在那里？对的，它只是一个装饰品。我们已经有足够的表达力来分辨两个分支，不过有了 else 似乎更加好看一些。很多语言里面都有 else 这个标记词在那里，所以我也把它放在那里。

这只是一个最简单的例子，其实那两个代码块里面不止可以写一条语句。你可以有任意多的语句，就像这样：

t ->
if (t < 22)
{
    a = 4 + 3
    b = a * 2
    "hotpot"
}
else
{
    x = "ice cream"
    x
}

这段代码和之前是等价的，你知道为什么吗？

字符串

上面一节出现了一种我们之前没见过的东西，我为了简洁而没有介绍它。这两个分支的结果，也就是加上引号的 “hotpot” 和 “ice cream”，它们并不是数字，也不是其它语言构造，而是一种跟数字处于几乎同等地位的“数据类型”，叫做字符串（string）。字符串是我们在计算机里面表示人类语言的基本数据类型。

关于字符串，在这里我不想讲述更加细节的内容，我把对它的各种操作留到以后再讲，因为虽然字符串对于应用程序很重要，它却并不是计算机科学最关键最本质的内容。

很多计算机书籍一开头就讲很多对字符串的操作，导致初学者费很大功夫去做很多打印字符串的练习，结果几个星期之后还没学到“函数”之类最根本的概念。这是非常可惜的。

布尔值

我们之前的 if 语句的条件 t < 22 其实也是一个表达式，它叫做“布尔表达式”。你可以把小于号 < 看成是跟加法一类的“操作符”。它的输入是两个数值，输出是一个“布尔值”。什么是布尔值呢？布尔值只有两个：true 和 false，也就是“真”和“假”。

举个例子，如果 t 的值是 15，那么 t < 22 是成立的，那么它的值就是 true。如果 t 的值是 23，那么 t < 22 就不成立，那么它的值就是 false。是不是很好理解呢？

我们为什么需要“布尔值”这种东西呢？因为它的存在可以简化我们的思维。对于布尔值也有一些操作，这个我也不在这一章赘述，放到以后细讲。

计算的要素

好了，现在你已经掌握了计算机科学的几乎所有基本要素。每一个编程语言都包括这些构造：

基础的数值。比如整数，字符串，布尔值等。(基础的数据类型, 不属于语言的范畴
表达式。包括基本的算术表达式，嵌套的表达式。()
变量和赋值语句。
分支语句。
函数和函数调用。
(变量, 函数, 控制豫剧 ,表达式)

你也许可以感觉到，我是把这些构造按照“从小到大”的顺序排列的。这也许可以帮助你的理解。

现在你可以回想一下你对它们的印象。每当学习一种新的语言或者系统，你只需要在里面找到对应的构造，而不需要从头学习。这就是掌握所有程序语言的秘诀。这就像学开车一样，一旦你掌握了油门，刹车，换挡器，方向盘，速度表的功能和用法，你就学会了开所有的汽车，不管它是什么型号的汽车。

我们在这一章不仅理解了这些要素，而且为它们定义了一种我们自己的“语言”。显然这个语言只能在我们的头脑里运行，因为我们没有实现这个语言的系统。在后面的章节，我会逐渐的把我们这种语言映射到现有的多种语言里面，然后你就能掌握这些语言了。

但是请不要以为掌握了语言就学会了编程或者学会了计算机科学。掌握语言就像学会了各种汽车部件的工作原理。几分钟之内，初学者就能让车子移动，转弯，停止。可是完了之后你还需要学习交通规则，你需要许许多多的实战练习和经验，掌握各种复杂情况下的策略，才能成为一个合格的驾驶员。如果你想成为赛车手，那就还需要很多倍的努力。

但是请不要被我这些话吓到了，你没有那么多的竞争者。现在的情况是，世界上就没有很多合格的计算机科学驾驶员，更不要说把车开得流畅的赛车手。绝大部分的“程序员”连最基本的引擎，油门，刹车，方向盘的工作原理都不明白，思维方式就不对，所以根本没法独自上路，一上路就出车祸。很多人把过错归结在自己的车身上，以为换一辆车马上就能成为好的驾驶员。这是一种世界范围的计算机教育的失败。

在后面的章节，我会引导你成为一个合格的驾驶员，随便拿一辆车就能开好。

什么是计算

现在你掌握了计算所需要的基本元素，可是什么是计算呢？我好像仍然没有告诉你。这是一个很哲学的问题，不同的人可能会告诉你不同的结果。我试图从最广义的角度来告诉你这个问题的答案。

当你小时候用手指算 4+3，那是计算。如果后来你学会了打算盘，你用算盘算 4+3，那也是计算。后来你从我这里学到了表达式，变量，函数，调用，分支语句…… 在每一新的构造加入的过程中，你都在了解不同的计算。

所以从最广义来讲，计算就是“机械化的信息处理”。所谓机械化，你可以用手指算，可以用算盘，可以用计算器，或者计算机。这些机器里面可以有代码，也可以没有代码，全是电子线路，甚至可以是生物活动或者化学反应。不同的机器也可以有不同的计算功能，不同的速度和性能……

有这么多种计算的事实不免让人困惑，总害怕少了点什么，其实你可以安心。如果你掌握了上一节的“计算要素”，那么你就掌握了几乎所有类型的计算系统所需要的东西。你在后面所需要做的只是加深这种理解，并且把它“对应”到现实世界遇到的各种计算机器里面。

为什么你可以相信计算机科学的精华就只有这些呢？因为计算就是处理信息，信息有它诞生的位置（输入设备，固定数值），它传输的方式（赋值，函数调用，返回值），它被查看的地方（分支）。你想不出对于信息还有什么其它的操作，所以你就很安心的相信了，这就是计算机科学这种“棋类游戏”的全部规则。